Геометрия

Геометрический объект (геометрия) представляет собой описательную структуру данных, на базе которой формируется графическое представление векторного элемента. Оно может быть частью визуального представления объектов реального мира. В зависимости от целей, геометрия может содержать данные о системе координат, в которой она создана.

Типы

ГИС Аксиома поддерживает следующие типы геометрических объектов:

Простые типы геометрии:

• Точка

• Полилиния

• Полигон

Коллекции:

• Смешанная коллекция

• Коллекция точек

• Коллекция полилиний

• Коллекция полигонов

Так же возможна работа с типами данных MapInfo:

• Линия

• Прямоугольник

• Скругленный прямоугольник

• Эллипс

• Дуга

• Текст

Рассмотрим подробнее геометрические типы. Переменные из примеров создания объектов будут использованы ниже в примерах более общего характера. Более общие характеристики объектов, а так же операции над ними будут рассмотрены ниже.

Точка

Точка представлена классом axipy.Point. Для нее характерно отсутствие таких параметров, как площади и линейных размеров. Создадим точку с координатами (10, 10) в СК Широта/Долгота. С целью визуального восприятия, результат представим в виде WKT строки (axipy.Geometry.to_wkt()).

cs = CoordSystem.from_prj("1, 104")
point = Point(10, 10, cs)
print('Точка ({}, {})'.format(point.x, point.y))
'''
>>> Точка (10, 10)
'''

Полилиния

Представлена классом axipy.LineString в виде непрерывной линии, соединяющей последовательность узлов. Для нее так же характерно отсутствие площади, но присутствует длина. Точки полилинии хранятся в виде списка list [ axipy.utl.Pnt ], то при задании, помимо передачи в конструктор такого списка, так же допустимо указание координат в виде пар координат tuple. Нумерация точек при доступе по индексу начинается с 0. Доступны через свойство axipy.LineString.points Приведем пример: создадим полилинию без СК. В этом же примере заменим 3-ю вершину на другое значение и выведем полученный результат в виде wkt axipy.Geometry.to_wkt():

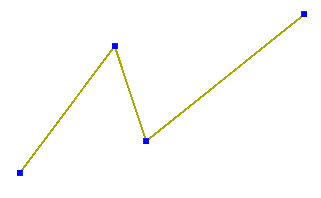
ls = LineString([(1, 1), (4, 5), (5, 2), (10, 6)])
ls.points[2] = (6, 3)
print(ls.to_wkt())
'''
>>> LINESTRING (1 1, 4 5, 6 3, 10 6)
'''

Так же присутствует возможность изменения существующих параметров полилинии. Добавим точку в позицию 1 и удалим точку 2:

ls.points.insert(1, (3, 6))
ls.points.remove(2)
print(ls.to_wkt())
'''
>>> LINESTRING (1 1, 3 6, 6 3, 10 6)
'''

Поддерживается инициализация через существующий итератор. Смоделируем данную ситуацию: создадим итератор на базе точек первой полилинии и на его основе создадим полилинию:

itr = (a for a in ls.points)
ls_it = LineString(itr)

Полигон

Представлен классом axipy.Polygon. Полигон представляет собой площадной объект, или другими словами часть плоскости, ограниченная замкнутой полилинией. Кроме внешней границы, полигон может иметь одну или несколько внутренних (дырок). Ему присущи такие свойства, как длина (периметр) и площадь. Точки хранятся по аналогии с полилинией. И инициализация в конструкторе или при добавлении дырки в полигон производится по подобному принципу. Характерной особенностью является тот факт, что все контуры замкнуты и последняя точка совпадает с первой. Это касается как формы полигона, так и его дырок. В качестве примера создадим полигон:

polygon = Polygon((1, 1), (2, 7), (8, 7), (7, 3))
print(polygon.to_wkt())
'''
>>> POLYGON ((1 1, 2 7, 8 7, 7 3, 1 1))
'''

И добавим в него две дырки:

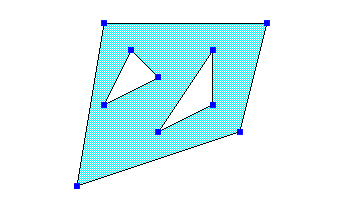
polygon.holes.append((2, 4), (3, 6), (4, 5))
polygon.holes.append((4, 3), (6, 6), (6, 4))
print(polygon.to_wkt())
'''
>>> POLYGON ((1 1, 2 7, 8 7, 7 3, 1 1), (2 4, 3 6, 4 5, 2 4), (4 3, 6 6, 6 4, 4 3))
'''

Как уже указывалось выше, работа с точками для полигона производится аналогично с полилинией. Это же касается и дырок, только доступ производится через свойство axipy.Polygon.holes Обновим значение третьей точки для второй дырки.

polygon.holes[1][2] = (6, 3)
print(polygon.to_wkt())
'''
>>> POLYGON ((1 1, 2 7, 8 7, 7 3, 1 1), (2 4, 3 6, 4 5, 2 4), (4 3, 6 6, 6 3, 4 3))
'''

Смешанная коллекция

Представлена классом axipy.GeometryCollection. Это нетипизированная коллекция. Может содержать внутри себя геометрии различных типов за исключением коллекций. Попробуем создать коллекцию и добавить в нее последовательно точку, полилинию и полигон. Стоит обратить внимание, что если добавляется последовательность точек, то она рассматривается как полилиния, в тоже время для указания полигона необходимо явно указать принадлежность к классу. Доступ к элементам коллекции производится по индексу, начиная со значения 0.

coll = GeometryCollection()
coll.append(1, 2)  # Точка
coll.append((3, 4), (5, 5), (10, 0))  # Полилиния
coll.append(Polygon((3, 4), (5, 5), (10, 0)))  # Полигон
print(coll.to_wkt())
'''
>>> GEOMETRYCOLLECTION (POINT (1 2), LINESTRING (3 4, 5 5, 10 0), POLYGON ((3 4, 5 5, 10 0, 3 4)))
'''

Удалим из коллекции полилинию и полигон, а после этого добавим объекты, созданные в предыдущих примерах. Точку поменяем простой заменой по индексу:

coll.remove(2)
coll.remove(1)
coll.append(polygon)
coll.append(ls)
coll[0] = point
print(coll.to_wkt())
'''
>>> GEOMETRYCOLLECTION (POINT (10 10), POLYGON ((1 1, 2 7, 8 7, 7 3, 1 1), (2 4, 3 6, 4 5, 2 4), (4 3, 6 6, 6 3, 4 3)), LINESTRING (1 1, 3 6, 6 3, 10 6))
'''

При замене элемента с заданием координат работают такие же принципы, как и в конструкторе. Обновим полилинию и полигон:

coll[2] = [(101, 102), (103, 104), (105, 106)]
coll[1] = Polygon((101, 102), (103, 104), (105, 106))
print(coll.to_wkt())
'''
>>> GEOMETRYCOLLECTION (POINT (10 10), POLYGON ((101 102, 103 104, 105 106, 101 102)), LINESTRING (101 102, 103 104, 105 106))
'''

Поменяем первую (она же последняя) точку полигона:

coll[1].points[0] = (0, 0)
print(coll.to_wkt())
'''
>>> GEOMETRYCOLLECTION (POINT (10 10), POLYGON ((0 0, 103 104, 105 106, 0 0)), LINESTRING (101 102, 103 104, 105 106))
'''

Далее рассмотрим типизированные коллекции. Принципы работы аналогичны нетипизированным, за исключением того, что позволено хранение геометрий только одного типа.

Коллекция точек

Представлена классом axipy.MultiPoint. Это типизированная коллекция. Допустимо хранение только точек. Создадим коллекцию точек и добавим в нее 2 элемента разными способами:

mpoint = MultiPoint()
mpoint.append(11, 11)
mpoint.append((12, 12))
mpoint.append(point)
print(mpoint.to_wkt())
'''
>>> MULTIPOINT (11 11, 12 12, 10 10)
'''

Коллекция полилиний

Представлена классом axipy.MultiLineString. Это типизированная коллекция. Допустимо хранение только полилиний.

mls = MultiLineString()  # Создадим саму коллекцию.
mls.append((11, 12), (13, 14), (15, 16))  # Добавим как объект
mls.append([(21, 22), (23, 24), (25, 26)])  # Добавим как перечень точек
print(mls.to_wkt())
'''
>>> MULTILINESTRING ((11 12, 13 14, 15 16), (21 22, 23 24, 25 26))
'''

Коллекция полигонов

Представлена классом axipy.MultiPolygon. Это типизированная коллекция. Допустимо хранение только полигонов. Отдельно стоит отметить, что при добавлении/изменения геометрий в виде перечня точек, в отличие от смешанной коллекции и коллекции полилиний, в данном случае создается полигон. Рассмотрим на примере:

mpoly = MultiPolygon()
mpoly.append((1, 2), (3, 4), (5, 6), (7, 8))
mpoly.append(polygon)  # Добавим ранее созданный с дыркой
print(mpoly.to_wkt())
''''
>>> MULTIPOLYGON (((1 2, 3 4, 5 6, 7 8, 1 2)), ((0 0, 1 10, 14 15, 11 5, 10 2, 0 0), (2 2, 44 44, 5 3, 2 2), (2 2, 2 4, 5 3, 2 2)))
'''

Далее рассмотрим объекты MapInfo. Одна из особенностей заключается в том, что они нестандартные, и, как следствие, не поддерживают WKT представление.

Линия

Представлена классом axipy.Line. Линейный объект. Описывается двумя точками: начальным и конечным узлом. Создадим линию, передав в конструктор пару точек. После этого последовательно поменяем координаты начала и конца линии.

line = Line((11, 11), (21, 21))
line.begin = (12, 12)
line.end = (120, 120)

Прямоугольник

Представлен классом axipy.mi.Rectangle. Площадной объект. Описывается минимальными и максимальными значениями по координатам X и Y. Создадим прямоугольник, задав параметры через конструктор. Затем поменяем предельные значения по X координате. Результат проконтролируем выводом значения axipy.Geometry.bounds геометрии.

rectangle = Rectangle(0, 0, 40, 20)
rectangle.xmin = 10
rectangle.xmax = 50
print(rectangle.bounds)
'''
>>> (10.0 0.0) (50.0 20.0)
'''

Скругленный прямоугольник

Представлен классом axipy.mi.RoundRectangle. Так же является площадным объектом. Отличительной особенностью от прямоугольника является наличие скруглений на углах. В остальном данные объекты аналогичны. Во избежании путаницы с параметрами, в конструкторе задается axipy.utl.Rect и радиусы скругления:

rrectangle = RoundRectangle([0, 0, 40, 20], 0.2, 0.2)
rrectangle.xRadius = 0.3
print(repr(rrectangle))
'''
>>> RoundRectangle xmin=0.0 ymin=0.0 xmax=40.0 ymax=20.0 xraduis=0.3 yraduis=0.2
'''

Эллипс

Представлен классом axipy.mi.Ellipse. Является площадным объектом. Создадим эллипс, передав в конструктор его Rect. После этого поменяем свойства.

ellipse = Ellipse([0, 0, 22, 33])
ellipse.center = (10, 10)  # Переопределим центр
ellipse.majorSemiAxis = 10  # Задание большой полуоси
ellipse.minorSemiAxis = 5  # Задание малой полуоси
print(ellipse.bounds)
'''
>>> (0.0 5.0) (20.0 15.0)
'''

Дуга

Представлена классом axipy.mi.Arc. Линейный объект. Задается в конструкторе через axipy.utl.Rect и, дополнительно, начальный и конечный угол дуги. Создадим объект, затем выведем основные свойства:

arc = Arc(Rect(0, 0, 20, 30), 45, 270)
print('center={} start={} end={}'.format(arc.center, arc.startAngle, arc.endAngle))
'''
>>> center=(10.0 15.0) start=45.0 end=270.0
'''

Текст

Представлен классом axipy.mi.Text. В отличие от описанных выше типов, его геометрические свойства определяются не только параметрами класса, но и параметрами его оформления.

rv = view_manager.create_reportview()
rect = Rect(8, 6, 11, 7)
text = Text("Пример", rect, view=rv)
geomItem = GeometryReportItem()
geomItem.geometry = text
geomItem.style = Style.for_geometry(text)
rv.report.items.add(geomItem)

Рассмотрим общие свойства геометрии.

Свойства геометрии

В зависимости от типа объекта, для него могут быть получены свойства. Продемонстрируем использование некоторых из них:

polygon = Polygon((0, 0), (0, 10), (10, 10), (10, 0))
print(f'Название: {polygon.name}')
print(f'Площадь: {polygon.get_area()}')
print(f'Периметр: {polygon.get_length()}')
print(f'Ограничивающий пряямоугольник: {polygon.bounds}')
'''
>>> Название: Полигон
>>> Площадь: 100.0
>>> Периметр: 40.0
>>> Ограничивающий пряямоугольник: (0.0 0.0) (10.0 10.0)
'''

Сериализация

ГИС Аксиома позволяет производить сериализацию геометрию в форматы текстового WKT или бинарного вида WKB. Подробнее

Рассмотрим на примере точечного объекта сначала для случая WKT. Будем использовать метод axipy.Geometry.from_wkt() для получения объекта из WKT и метод axipy.Geometry.to_wkt() для получения WKT представления полученного объекта:

polygon = Geometry.from_wkt('POLYGON ((10 10, 100 100, 100 10, 10 10))')
point = Geometry.from_wkt('SRID=4326;POINT (10 10)')
crs = CoordSystem.from_epsg(4326)
pline = Geometry.from_wkt('LINESTRING (30 10, 10 30, 40 40)', crs)

Аналогично проделаем для WKB. При этом используются, соответственно, axipy.Geometry.from_wkb() и axipy.Geometry.to_wkb():

wkb = b'\x01\x01\x00\x00\x00\x00\x00\x00\x00\x00\x00$@\x00\x00\x00\x00\x00\x00$@'
pnt = Geometry.from_wkb(wkb)

Преобразования

Для перепроецирование в другую СК используется метод axipy.Geometry.reproject(). Заметим, что исходный объект должен содержать свою СК. В рамках примера перепроецируем точку из СК Широта/Долгота в проекцию Меркатора:

csLL = CoordSystem.from_prj("1, 104")
csMercator = CoordSystem.from_prj("10, 104, 7, 0")
point_ll = Point(10, 10, csLL)
point_merc = point_ll.reproject(csMercator)
print('point result: {}'.format(point_merc.to_wkt()))
'''
>>> point result: POINT (1113194.90793274 1111475.10285222)
'''

Более простые преобразования типа сдвига axipy.Geometry.shift(), масштабирования axipy.Geometry.scale() и поворот axipy.Geometry.scale() игнорируют указанную СК и данные операции производятся в текущих координатах объекта. Рассмотрим на примерах:

polygon = Polygon((1, 1), (2, 7), (8, 7), (7, 3))
polygon_shift = polygon.shift(5, 5)
# Сдвинем на величину 5 по X и Y
print('polygon shift: {}'.format(polygon_shift.to_wkt()))
polygon_scale = polygon.scale(5, 5)
# Отмасштабируем координаты относительно центра
print('polygon scale: {}'.format(polygon_scale.to_wkt()))
# Повернем на 90 градусов против часовой стрелки относительно точки (10, 40)
polygon_rotated = polygon.rotate((10, 40), 90)
print('polygon rotate: {}'.format(polygon_rotated.to_wkt()))
'''
>>> polygon shift: POLYGON ((6 6, 7 12, 13 12, 12 8, 6 6))
>>> polygon scale: POLYGON ((-13 -11, -8 19, 22 19, 17 -1, -13 -11))
>>> polygon rotate: POLYGON ((49 31, 43 32, 43 38, 47 37, 49 31))
'''

Для более сложных аффинных преобразований можно использовать axipy.Geometry.affine_transform() с указанием матрицы преобразований QTransform

Пространственные операции

Нормализация объекта

Для проверки валидности геометрии предусмотрено свойство axipy.Geometry.is_valid. Если геометрия не проходит тест на валидность (данное свойство False), то для его нормализации используется метод axipy.Geometry.normalize(). Краткую аннотацию причины почему геометрия недействительна, можно воспользовавшись свойством axipy.Geometry.is_valid_reason.

Создадим заведомо неправильный полигон и попробуем его исправить:

poly_bad = Polygon([(1, 1), (6, 7), (6, 1), (1, 7)])
poly_norm = poly_bad.normalize()
print('Validate source: {} ({})'.format(poly_bad.is_valid, poly_bad.is_valid_reason))
print('Validate destination: {}'.format(poly_norm.is_valid))
print('Wkt:{}'.format(poly_norm.to_wkt()))
'''
>>> Validate source: False (Self-intersection[3.5 4])
>>> Validate destination: True
>>> Wkt:MULTIPOLYGON (((3.5 4, 1 1, 1 7, 3.5 4)), ((3.5 4, 6 7, 6 1, 3.5 4)))
'''

В результате мы получили коллекцию из двух полигонов.

Клонирование объекта

Для создания копии объекта используется метод axipy.Geometry.clone():

point1 = Point(10, 10)
point2 = point1.clone()
point1.x = 12
print('>>>', point1.to_wkt(), point2.to_wkt())
'''
>>> POINT (12 10) POINT (10 10)
'''

Логические операции

Пространственные отношения, возвращающие логический True или False:

Точное совпадение геометрий производится посредством axipy.Geometry.equals(), если же необходимо произвести приблизительное сравнение, то используем метод axipy.Geometry.almost_equals():

polygon1 = Polygon((1, 1), (2, 7), (7, 3))
polygon2 = Polygon((1, 1.1), (2, 7), (7, 3))
print('Точное сравнение:', polygon1.equals(polygon2))
print('Сравнение с точностью 0.2:', polygon1.almost_equals(polygon2, 0.2))
'''
>>> Точное сравнение: False
>>> Сравнение с точностью 0.2: True
'''

Проверка на попадание axipy.Geometry.contains()

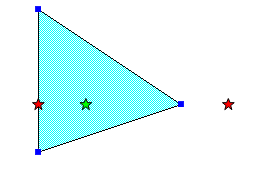
poly1 = Polygon((1, 1), (1, 7), (7, 3))
point1 = Point(3, 3)
point2 = Point(9, 3)
point3 = Point(1, 3)
print('Точка внутри:', poly1.contains(point1))
print('Точка снаружи:', poly1.contains(point2))
print('Точка на грани:', poly1.contains(point3))
'''
>>> Точка внутри: True
>>> Точка снаружи: False
>>> Точка на грани: False
'''

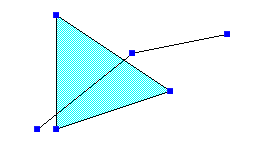
Проверка на частичное пересечение axipy.Geometry.crosses()

poly1 = Polygon((1, 1), (1, 7), (7, 3))
sl = LineString((0, 1), (5, 5), (10, 6))
print(poly1.crosses(sl))
'''
>>> True
'''

Проверка на отсутствие соприкосновений axipy.Geometry.disjoint()

print(poly1.disjoint(sl))
'''
>>> False
'''

Проверка пересечений объектов axipy.Geometry.intersects()

Пересечение геометрий, если результат отличен от анализируемых данных axipy.Geometry.overlaps()

poly2 = Polygon((5, 1), (4, 4), (10, 3))
print(poly1.overlaps(poly2))
'''
>>> True
'''

Проверка касания axipy.Geometry.touches()

point3 = Point(1, 5)
print('Точка на грани:', poly1.touches(point3))
'''
>>> True
'''

Функция, обратная contains axipy.Geometry.within()

print('Точка внутри:', Point(2, 5).within(poly1))
''''
>>> True
'''

Охват одной геометрии другой axipy.Geometry.covers()

Отношения DE-9IM

Функция axipy.Geometry.relate() проверяет все DE-9IM отношения между объектами. Предикаты выше являются их частными случаями.

print('relate:', poly1.relate(Point(10, 10)))
'''
relate: FF2FF10F2
'''

Операции над объектами

В данном разделе рассмотрим операции, результатом выполнения которых будут новые объекты.

Получение границ геометрии в виде полилинии axipy.Geometry.boundary()

poly = Geometry.from_wkt('POLYGON ((1 1, 2 7, 8 7, 7 3, 1 1), (2 4, 3 6, 4 5, 2 4), (4 3, 6 6, 6 4, 4 3))')
poly_boundary = poly.boundary()
print(poly_boundary.to_wkt())
'''
>>> MULTILINESTRING ((1 1, 2 7, 8 7, 7 3, 1 1), (2 4, 3 6, 4 5, 2 4), (4 3, 6 6, 6 4, 4 3))
'''

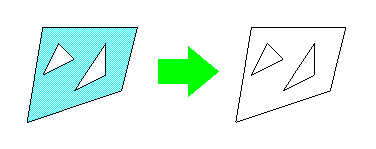
Центроид объекта axipy.Geometry.centroid()

centroid = poly.centroid()
print(centroid.to_wkt())
'''
>>> POINT (4 4.5)
'''

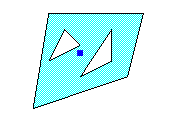
Вычитание объектов axipy.Geometry.difference()

poly1 = Polygon((1, 1), (1, 7), (7, 3))
poly2 = Polygon((5, 1), (4, 4), (10, 3))
print(poly1.difference(poly2).to_wkt())
'''
>>> POLYGON ((1 1, 1 7, 6 3.67, 4 4, 4.6 2.2, 1 1))
'''

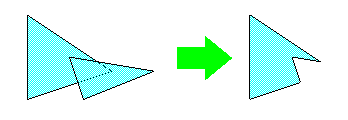
Пересечение объектов axipy.Geometry.intersection()

print(poly1.intersection(poly2).to_wkt())
'''
>>> POLYGON ((6 3.67, 7 3, 4.6 2.2, 4 4, 6 3.67))
'''

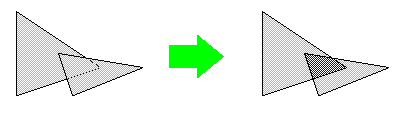
Обратное пересечение объектов axipy.Geometry.symmetric_difference()

print(poly1.symmetric_difference(poly2).to_wkt())
'''
>>> MULTIPOLYGON (((1 1, 1 7, 6 3.67, 4 4, 4.6 2.2, 1 1)), ((4.6 2.2, 7 3, 6 3.67, 10 3, 5 1, 4.6 2.2)))
'''

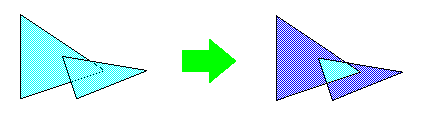
Объединение объектов axipy.Geometry.union()

print(poly1.union(poly2).to_wkt())
'''
>>> POLYGON ((1 1, 1 7, 6 3.67, 10 3, 5 1, 4.6 2.2, 1 1))
'''

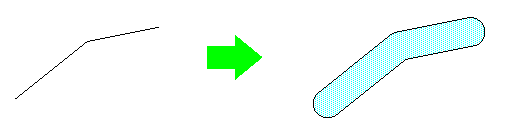
Построение буфера axipy.Geometry.buffer()

sl = LineString((0, 1), (5, 5), (10, 6))
buf = sl.buffer(1)

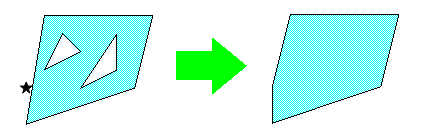
Границы объекта axipy.Geometry.convex_hull()

Рассмотрим на примере коллекции:

coll = GeometryCollection()
coll.append(polygon)
coll.append(Point(1, 5))
print(coll.convex_hull().to_wkt())
'''
POLYGON ((1 1, 1 5, 2 7, 8 7, 7 3, 1 1))
'''

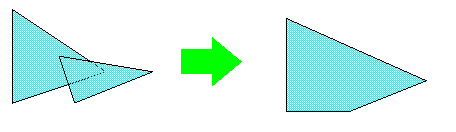
Пример с внутренними углами:

print(poly1.union(poly2).convex_hull().to_wkt())
'''
POLYGON ((1 1, 1 7, 10 3, 5 1, 1 1))
'''

Прямоугольные границы объекта axipy.Geometry.envelope()

print(coll.envelope().to_wkt())
'''
POLYGON ((1 1, 8 1, 8 7, 1 7, 1 1))
'''

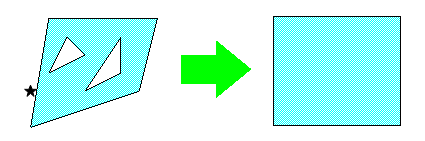
Конвертация объектов

Пример конвертации полигона в полилинию.

polygon = Polygon((0, 0), (0, 10), (10, 10))
print(polygon.to_linestring().to_wkt())
'''
>>> LINESTRING (0 0, 0 10, 10 10, 0 0)
'''

Пример конвертации полилинии в полигон.

ls = LineString((0, 0), (0, 10), (10, 10))
print(ls.to_polygon().to_wkt())
'''
>>> POLYGON ((0 0, 0 10, 10 10, 0 0))
'''